Lorsque la bulle se détache de son site de nucléation, elle prend naturellement une forme sphérique car c'est la forme qui, à un volume donné, présente la plus petite surface et donc la plus petite dépense d'énergie. Cette bulle est soumise à plusieurs forces*1 qui vont provoquer son ascension.
La première force que nous allons étudier est la poussée d'Archimède*2. Avant de commencer, nous allons calculer le volume de la bulle lors de sa sortie de la fibre, c'est-à-dire lorsque son rayon mesure entre 5.0 et 10.0 µm, soit entre 5.0×10-6 et 1.00×10-5 m (nos calculs sont basés sur la plus petite valeur).
Vsphère = 4/3 × π × R3 Avec V en m3 et R en m
Vsphère = 4/3 × π × (5.0×10-6 )3 = 5.2 × 10-16 m3 soit 5.2 × 10-13 L
Après avoir obtenu le volume d'une bulle lors de sa sortie de la fibre , nous pouvons calculer la poussée d’Archimède qu'elle subit :
Π = ρ × g × V Avec Π en N, ρ en kg.L-1, V en L et g constante = 9.81 N.kg-1
-
Π la poussée d'Archimède
-
ρ la masse volumique du champagne : ρ = 0.998 kg.L-1
-
g la valeur de la pesanteur terrestre
-
V le volume de la bulle :ici, V = 5.2 × 10-13 L
Π = 0.998 × 9.81 × 5.2 × 10-13 = 5.1×10-12 N
Néanmoins, nous savons que le volume de la bulle augmente au cours de son ascension, ce qui a comme conséquence d'augmenter la puissance de la poussée d'Archimède (en effet, si V augmente, alors Π augmente, comme nous pouvons le voir sur la formule ci-dessus).
La seconde force que nous allons étudier est la force de frottement. Selon la formule de Stokes :
f = 6π × η × R × v Avec f en N, η en N.s.m-2, R en m et v en m.s-1
-
η la viscosité du champagne : η = 1.5×10-3 N.s.m-2
-
R le rayon de la bulle, ici : R = 5.0×10-6 m
-
v la vitesse de la bulle, compris entre 2.0×10-5 et 5.0×10-5 m.s-1, soit une moyenne de
3.5×10-5 m.s-1
f = 6π × 1.5×10-3 × 5.0×10-6 × 3.5×10-5
f = 4.9×10-12 N
Remarque : L'unité S.I. de la viscosité est le Pa.s ; toutefois, par souci de cohérence des unités, nous la convertissons ici en N.s.m-2 .
Avant de pouvoir comprendre le rôle de cette force au cours de l'ascension, il nous faut aborder une notion nouvelle : la vitesse*3 de la bulle. Pour la mesurer, nous avons mené l'expérience suivante :
Nous avons versé du champagne dans une éprouvette graduée et nous avons filmé le comportement des bulles grâce à une caméra grande vitesse. Nous avons ensuite pointé la trajectoire*4 d'une bulle à l'aide du logiciel REGAVI. Les résultats obtenus sont les suivants :
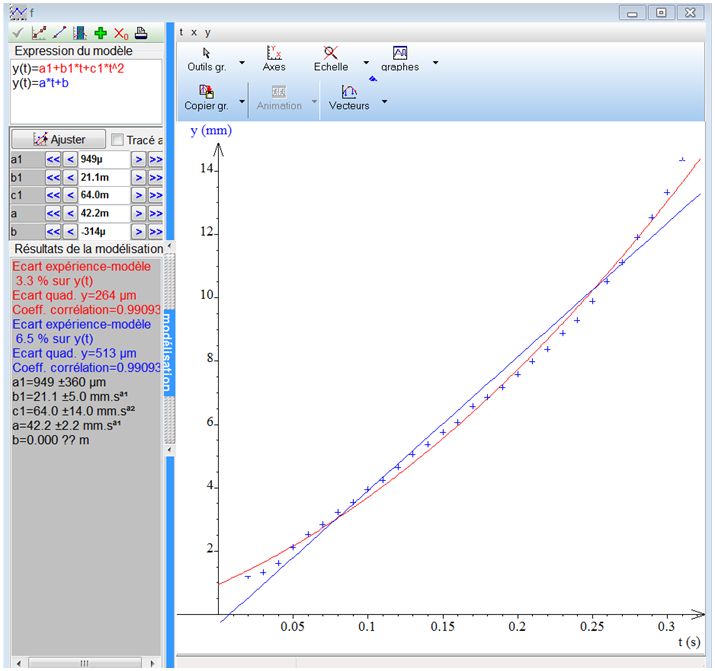
Au lieu d'obtenir une droite (en bleu) qui aurait signifié que la vitesse est constante*5, nous avons obtenu des résultats s'approchant d'une parabole (en rouge), ce qui nous indique que la vitesse augmente au cours de l'ascension. Pour résoudre ce problème,voici la loi des gaz parfaits :
P × V = n × R × T Avec P en Pa, V en m3, n en mol, T en K et
R constante = 8.31 J.K-1.mol-1
Nous savons ici que le volume V augmente ; en outre, R et la température T sont constantes (ici, T = 282 K, soit 9°C). Cette augmentation de volume ne peut donc être causée que par deux choses : une diminution de la pression P ou une augmentation de la quantité de matière n. La pression passant de 6.0×105 à 1.0×105 Pa de façon quasi-instantanée, elle ne peut donc être la raison du changement de volume de la bulle.
Ainsi, c'est la quantité de matière qui augmente : tout au long de sa remontée, la bulle se charge en dioxyde de carbone présent autour d’elle et grossit de plus en plus en l’aspirant. En moyenne, elle passe de 5.0 µm de rayon lors de sa sortie de son site de nucléation et peut atteindre jusqu'à 0.50 mm de rayon à son arrivée à la surface : son volume est multiplié par 1 million lors de son ascension.
Encore une fois, la force étudiée présente des facteurs qui varient au cours de l'ascension, notamment le rayon, mais aussi la vitesse, comme nous venons de le démontrer. On peut donc en conclure que la force de frottement augmente au cours de l'ascension de la bulle. Toutefois, nous verrons plus tard que cette force se compense grâce à la présence de certaines molécules.
Enfin, la dernière force que nous allons étudier est le poids d'une bulle. Avant d'appliquer la formule, nous avons besoin de la masse d'une bulle (ici, nous travaillons sur la bulle juste sortie du fibre) :
ρ = m / V Avec ρ en kg.m-3, m en kg et V en m3
1.87 = m / 5.2×10-16 soit m = 1.87 × 5.2×10-16 = 9.7×10-16 kg
La formule pour calculer le poids est la suivante :
p = m × g Avec p en N, m en kg et g constante = 9.81 N.kg-1
p = 9.7×10-16 × 9.81 = 9.5×10-15 N
Le poids de la bulle dépendant du rayon de celle-ci, nous pouvons en déduire que cette force aussi augmente au cours de l'ascension de la bulle.
La poussée d'Archimède a une direction verticale et un sens de bas en haut, contrairement à la force de frottement et au poids, qui ont une direction verticale et un sens de haut en bas. Cependant, la bulle monte : nous pouvons facilement expliquer ce phénomène par ce calcul :
f + p < Π soit 4.9×10-12 + 9.5×10-15 < 5.1×10-12
4.9×10-12 N < 5.1×10-12 N

Bilan des forces
Ainsi, la somme des forces de sens de haut en bas est plus faible que la poussée d'Archimède : la bulle monte. Les forces contraires à cette poussée deviennent négligeables car du CO2 est absorbé tout au long de l'ascension, ce qui provoque l'accélération de la bulle (elle se stabilise après avoir atteint une vitesse moyenne de 15 à 20 cm.s-1, soit 0.5 km.h-1). Il existe d'autres forces telles que la masse ajoutée, mais elles présentent un impact trop faible pour avoir un rôle vraiment important dans l'ascension de la bulle.
TENSIOACTIFS
Il existe dans le champagne des molécules dites tensioactives. Elles sont fabriquées par le raisin et les levures et apparaissent sous forme de protéines et de glycoprotéines pendant la fabrication. Ces molécules ont la particularité d’être à doubles affinités soit une extrémité hydrophobe (qui est repoussée par l'eau) mais également une extrémité hydrophile (qui est attirée par l'eau). La bulle est donc une surface parfaite pour ces molécules, car elle est l'interface liquide/gaz (en l’occurrence, ce gaz est le CO2). La queue hydrophobe va donc venir se coller à la bulle, tandis que sa tête va rester au contact du champagne, et ce durant toute l'ascension de la bulle vers la surface

Molécule tensioactive
Les tensioactifs recouvrent une grande partie de la surface de la bulle, ce qui cause un changement dans le contact entre celle-ci et le liquide et provoque l'apparition de la force de frottement. Nous avons vu plus haut que le volume de la bulle augmente lors de son ascension, donc sa surface augmente, ce qui a pour effet de multiplier la quantité de tensioactifs sur la bulle.
Au début de l'ascension, la bulle a un faible rayon et une vitesse lente, ce qui permet aux molécules tensioactives de recouvrir l’intégralité de sa surface. La bulle est donc rigidifiée par les molécules. Puis le volume de la bulle augmente et sa vitesse aussi, donc les molécules tensioactives ne peuvent pas entièrement recouvrir la bulle, ce qui provoque une dilution des tensioactifs. Autrement dit, cette absence de molécules tensioactives a pour effet de fragiliser la bulle mais de réduire considérablement la force de frottement. A la fin de sa remontée, la bulle a atteint un volume maximal ainsi qu’une vitesse maximale mais la dilution des tensioactifs la rend totalement vulnérable et elle éclate à la surface.

De plus, la présence des tensioactifs est une autre raison de la forme des bulles : afin de réduire la surface de contact entre les deux milieux (liquide /gaz), la bulle va prendre une forme sphérique.
Parfois, durant leur ascension, il peut y avoir collision*6 entre deux bulles. Cela peut se passer de deux manières différentes : soit elles rebondissent puis se repoussent afin continuer leurs routes, soit, dans les cas où ces bulles sont pauvres en molécules tensioactives, elles fusionnent*7 afin de former une seule et même bulle.
Force*1 : puissance ou action d’un facteur physique
Archimède*2 : homme scientifique grec ayant vécu dans l’Antiquité
Vitesse*3 : célérité, rapidité dans l’action
Trajectoire*4 : ligne qui décrit le mouvement
Constante*5 : valeur inchangée, qui dure
Collision*6 : choc, impact
