When the bubble detaches from its nucleation site, it naturally takes a spherical shape, the shape for which for a given volume has the smallest surface area, and thus the lowest expenditure of energy. This bubble is subject to several forces that will cause its ascent.
The first one we are going to study is Archimedes' buoyant force. Before we begin, we must calculate the volume of the bubble the moment it gets ejected from the fiber, that is to say when its radius measures between 5.0 and 10.0 µm, (5.0×10-6 to 1.00×10-5 m ; taking here the lowest value):
Vsphere = 4/3 × π × R3 V in m3 and R in m
Vsphere = 4/3 × π × (5.0×10-6)3 = 5.2×10-16 m3 or 5.2×10-13 L
After obtaining the volume of a bubble just as it is ejected from the fiber, we can then calculate the buoyancy that it experiences:
Π = ρ × g × V Π in N, ρ in kg.L-1, V in L and g constant = 9.81 N.kg-1
- Π : Archimedes' buoyant force
- ρ : the volumetric mass or “density” of champagne : ρ = 0.988 kg.L-1
- g : the terrestrial gravity value
- V: the volume of the bubble: Here, V = 5.2×10-13 L
Π = 0.988 × 9.81 × 5.2×10-13= 5.1×10-12 N
We know that the volume of the bubble increases during its ascent, which results in an increase in the buoyant force (in fact, if the volume V increases, the buoyant force Π also increases as we can see from the above formula).
The second force that we will study is the friction force. According to Stokes' formula:
f = 6π × η × R × v f in N, η in N.s.m-2, R in m and v in m.s-1
- η: the viscosity of champagne: η = 1.5×10-3 N.s.m-2
- R: the radius of the bubble, here: R = 5.0×10-6 m
- v: the speed of the bubble, which can vary between 2.0×10-5 et 5.0×10-5 m.s-1, and therefore has a average of 3.5×10-5 m.s-1
f = 6π × 1.5×10-3 × 5.0×10-6 × 3.5×10-5
f = 4.9×10-12 N
Note: The SI unit of viscosity is Pa.s. However, for the sake of consistency of units, we converted it in N.s.m-2.
To understand the role of this force during the ascent, we must understand another concept: the speed of the bubble. To measure it, we conducted the following experiment:
We poured champagne into a graduated cylinder and filmed the behavior of the bubbles through a high-speed camera. We then studied the trajectory of a bubble thanks to the REGAVI software. Here are the results:
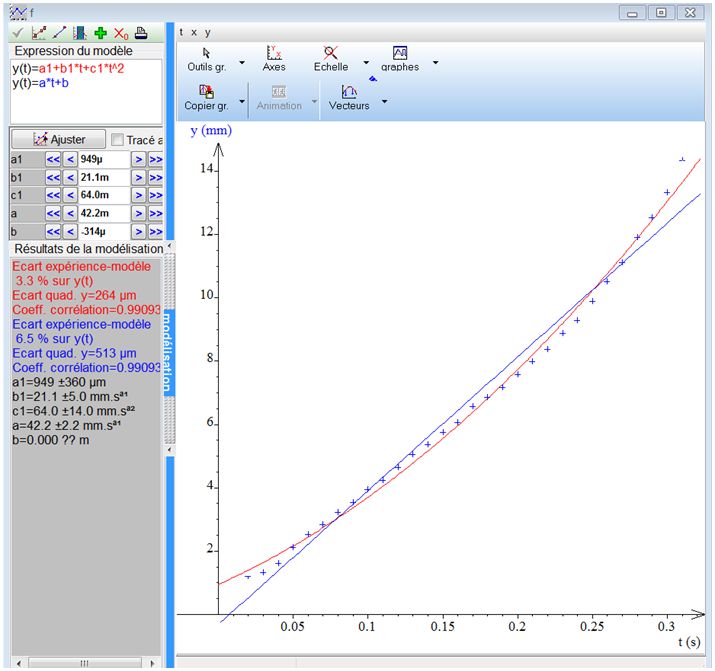
Instead of getting a straight line (in blue) which would mean that speed is constant, we obtained results approaching a parabola (in red), which indicates that the speed increases during the ascension. To solve this problem, we used the ideal gas law:
P × V = n × R × T P in Pa, V in m3, n in mol, T in K and
R constant = 8.31 J.K-1.mol-1
We know here that the volume V increases; in addition, the constant R and the temperature T are constant (here, T = 282 K, which is 9 ° C). The increase in volume can therefore only be caused by two things: a decrease in the pressure P or an increase in the amount of substance n. The pressure decreases from 6.0 × 105 Pa to 1.0 × 105 Pa almost instantaneously, the decrease in pressure can not be the reason for the bubble volume change.
Thus, it is the amount of substance which increases: throughout its ascent, the bubble charges itself with the CO2 found around it and swells more and more in proportion with the amount it takes in. On average, the radius of a bubble goes from 5.0 µm when it is released from its nucleation site and to up to 0.50 mm at its arrival at the surface: therefore, the bubble is multiplied a million times during its ascent.
The studied force involves varying factors during the ascent, including the radius but also the speed, as we just demonstrated. We can therefore conclude that the friction force increases during the ascent of the bubble. Notwithstanding, we will later see that this force compensates itself thanks to the presence of particular molecules.
Finally, the last force we will study is the weight of a bubble. Before applying the formula, we need to find the weight of a bubble (a bubble which has just been ejected from the fiber):
ρ = m / V ρ in kg m-3, m in kg and V in m3
- ρ: the volumetric mass/density of CO2; ρ = 1.87 kg.m-3
- V: the volume of the bubble; V = 5.2×10-16 m3
1.87 = m / 5.2×10-16 therefore m = 1.87 × 5.2×10-16 = 9.7×10-16 kg
The formula for calculating weight is the following:
p = m × g p in N, m in kg and g constant= 9.81N.kg-1
p = 9.7 ×10-16× 9.81 = 9.5 ×10-15 N
The weight of the bubble depends on its radius; therefore, we can deduce that this force also increases during the ascent of the bubble.
Buoyant force has a precise vertical direction from bottom to top, unlike the friction force and the weight, which have a precise vertical direction but from top to bottom. However, the bubble rises during its ascent: we can easily explain this phenomenon by this calculation:
f + p < Π or 4.9 ×10-12 + 9.5 ×10-15 < 5.1 ×10-12
4.9×10-12 N < 5.1×10-12 N
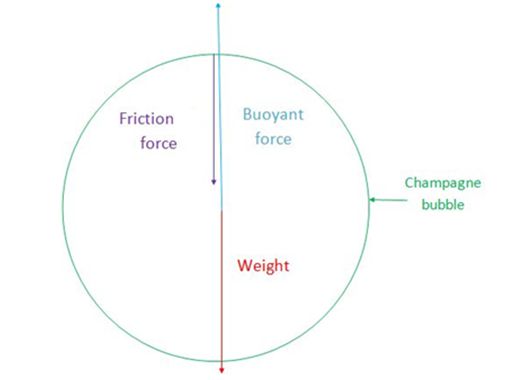
Balance between the different forces
The sum of the forces whose direction is from top to bottom is lower than the Archimedes’ buoyant force, which explains why the bubble rises. The forces contrary to it become negligible because CO2 is absorbed throughout the rise, causing the bubble to accelerate (it reaches and stabilizes at an average speed of 15 to 20 cm.s-1, or 0.5 km.h-1). There are other forces such as added mass, but they have too low an impact to have an important role in the rise of the bubble.
SURFACTANTS
Champagne contains molecules called surfactants. These molecules have the particularity of having a double affinity, with a hydrophobic end (which cannot withstand contact with water), and a hydrophilic end (which, on the contrary, seeks contact with water). The bubble is thus a perfect surface for these molecules because it is the liquid / gas interface (in this case, the gas is CO2). The hydrophobic tail sticks to the bubble, while the head stays in contact with the champagne and this throughout the whole ascension of the bubble to the surface.
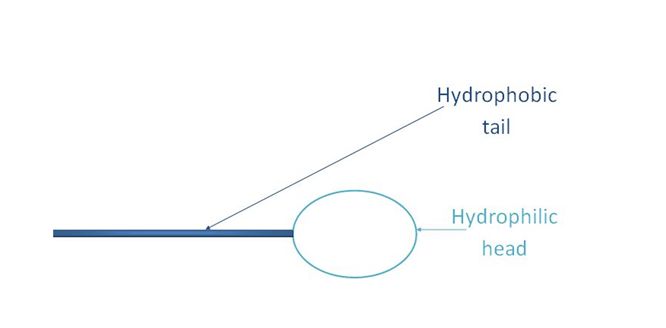
Surfactant Molecule
Surfactants cover a large part of the surface of the bubble, which causes a change in the contact between the bubble and the liquid and causes the appearance of friction force. We have seen above that the bubble volume increases during its ascent, therefore, its surface area is increased, resulting in an increase in the amount of surfactants on the bubble.
At the beginning of the ascent, the bubble has a low radius and a slow speed, allowing the surfactant molecules to cover its entire surface. The bubble is thus stiffened by the molecules. Then the volume and speed of the bubble increases until the surfactant molecules no longer fully cover the bubbleand this causes a dilution of the surfactants. In other words, this lack of surfactant molecules has the effect of weakening the bubble but also greatly reduces the friction force. When the bubble has reached its ascent, the bubble has a maximum volume and a maximum velocity, but the dilution of the surfactants renders the bubble completely vulnerable and it so it bursts at the surface.
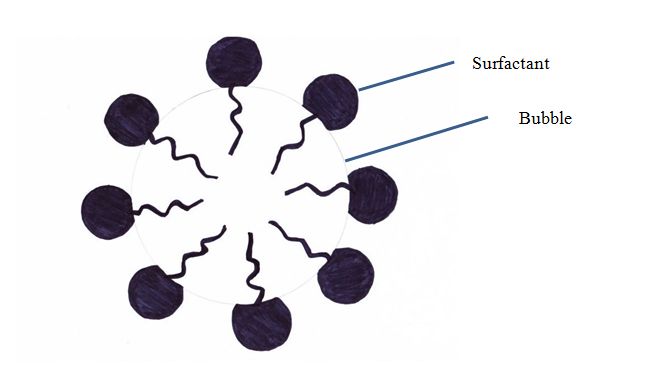
The presence of surfactants is another reason for the shape of bubbles: to reduce the contact surface between the two media (liquid/gas), takes a spherical shape.
A collision between two bubbles can sometimes happen during their ascent. This can happen in two different ways: either they rebound against each other and then continue their ascent individully; or, in cases where these bubbles are poor in surfactant molecules, they merge to form a single bubble.
